Step 7. Collect Information About the Current R Session.
Contact Us
The Centre for Artificial Intelligence Driven Drug Discovery (AIDD) at Macao Polytechnic University
Mediation Mendelian Randomization
Unraveling causal pathways: Understanding how exposures affect outcomes through mediating mechanisms using two-step MR analysis
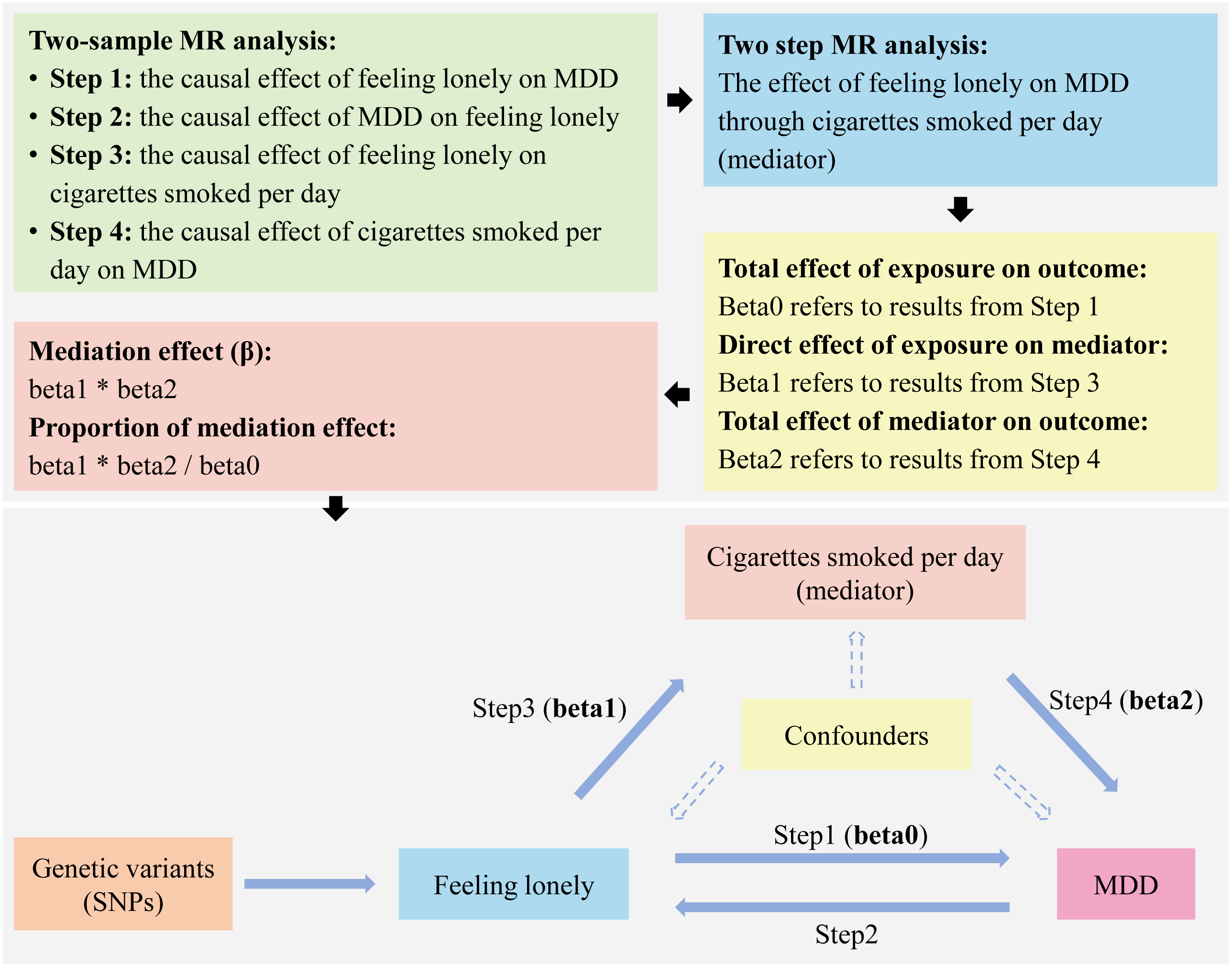
The main purpose of mediation MR is to investigate whether a mediator can mediate the effect of exposure on the outcome. It is generally applicable for identifying potential mechanisms underlying the relationship from exposure to outcome.
Analysis Steps
Exposure → Outcome
Direct causal effect estimation.
Identify significant SNPs from exposure GWAS, remove LD, extract from outcome GWAS.
Calculate total causal effect (β₀).
Exposure → Mediator
Exposure effect on mediator.
Use exposure SNPs to estimate causal effect on mediator, ensuring no direct
confounder relationships. Calculate effect (β₁).
Mediator → Outcome
Mediator effect on outcome.
Identify mediator SNPs, remove LD, extract from outcome GWAS.
Calculate mediator causal effect (β₂).
Results Interpretation
Effect Decomposition
Where β₀ is the total effect, β₁ is exposure→mediator effect, and β₂ is mediator→outcome effect.
Interpretation Scenarios:
If β₀, β₁, and β₂ are all significant: Causal association exists with partial mediation. Test if direct effect β₀ - (β₁ × β₂) significantly differs from 0.
If β₀ is not significant, but both β₁ and β₂ are significant: The association is entirely mediated by the mediator variable.
If β₀ is significant, but at least one of β₁ or β₂ is not significant: No mediating effect exists in the causal pathway.
Critical Considerations
Essential guidelines for responsible mediation MR analysis and interpretation
Methodological Rigor
While democratizing MR methodology is crucial, atheoretical applications pose significant risks. Avoid randomly selecting exposure-outcome pairs without biological justification or established hypotheses.
Best Practice: Ground analyses in well-defined, evidence-based hypotheses and adhere to established guidelines [1]. Consider biological plausibility, pleiotropic pathways, and implement comprehensive quality control including F-statistics evaluation and heterogeneity assessment.
1. Guidelines for performing Mendelian randomization investigations: update for summer 2023
Evidence Integration
MR results should never be interpreted in isolation. Robust causal inference requires integrating multiple analytical strategies and evidence sources.
Recommended Approach: Combine univariable MR (basic causal relationships), multivariable MR (controlling confounders), and mediation MR (causal pathways) with complementary analyses including colocalization, fine-mapping, and experimental validation. Treat MR as contributory evidence, not definitive proof.
Known Limitations
Methodological constraints require careful consideration during interpretation. Key limitations include population stratification differences, shared genetic architecture assumptions, and horizontal pleiotropy vulnerability.
Critical Issues: Sample overlap bias, differential LD patterns across populations, weak instrument bias, inability to model time-varying effects or non-linear relationships, and challenges in detecting pleiotropic effects using summary statistics. Statistical power depends on instrument strength and GWAS sample dimensions.